Problem sheet 1

Lecture: Introduction to general relativity, 2023-2024

Deadline: Nov 3rd, 2023 (3 weeks)

Topic: special relativity

Please send the solutions via email to korzynski@cft.edu.pl. I prefer PDF's (for example LaTeX-generated) or common graphic formats (for example scans of your hand-written notes).

Problem 1

Let $v$ be the velocity (standard 3-velocity) of an inertial frame $P$ with respect to another one, $Q$ . Define the rapidity $\theta$ as a dimensionless scalar given by

\theta(v) = \textrm{artanh}\, v,

or, equivalently, by the condition $v = \tanh \theta$ .

Prove that the Lorentz transformation matrix from $P$ to $Q$ in a two-dimentsional Minkowski space, with 2 spatial dimensions suppressed, takes the form of

\Lambda = \begin{pmatrix} \cosh \theta & -\sinh \theta \\ -\sinh\theta & \cosh\theta\end{pmatrix}.

Prove that $\theta(-v) = -\theta(v)$ .
Additivity of rapidity. Prove that if the inertial frame $B$ moves with respect to $A$ with rapidity $\theta_{AB}$ , while $C$ moves with respect to $B$ with rapidity $\theta_{BC},$ then $C$ moves with respect to $A$ with $\theta_{AC}$ given by

\theta_{AC} = \theta_{AB} + \theta_{BC}.

Problem 2

Derivation of the time dilation formula.

Consider a clock $C_P$ stationary in an inertial frame $P$ and another one, called $C_Q$ , stationary in $Q$ , see Fig. 1.

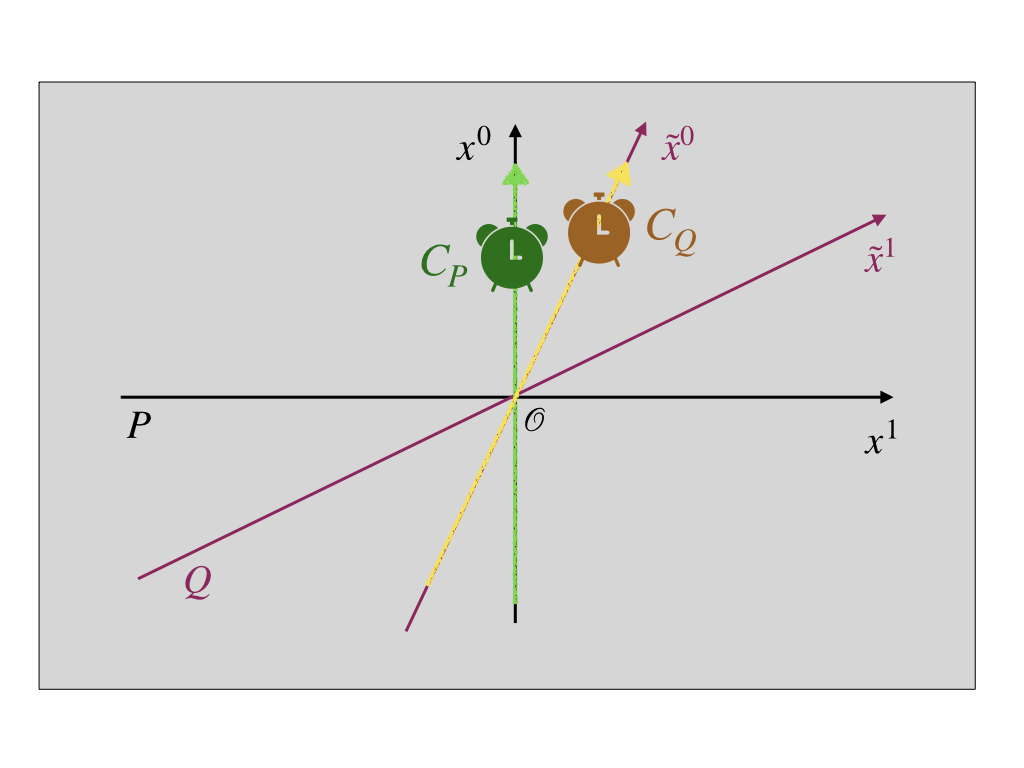$Q$ moves with respect to $P$ with velocity $v$ . Assume that both $C_P$ and $C_Q$ read 0 when the two clocks pass point $\cal O$ .

Calculate the coordinate time $x^0$ in $P$ of the moment when $C_Q$ reads a fixed time $t > 0$ . Show that $x^0 > t$ , i.e. clock $C_Q$ appears to run slower than $C_P$ for an observer in $P$ .
Calculate the coordinate time $\tilde x^0$ in $Q$ of the moment when $C_P$ reads the same time $t$ . Show that $\tilde x^0 > t$ , i.e. clock $C_P$ appears to run slower than $C_Q$ for an oberver in $Q$ .
Explain why the two results above are not contradictory.